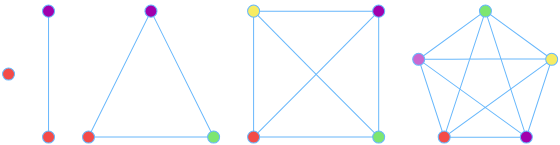
NP-полнота задачи о раскраске графа
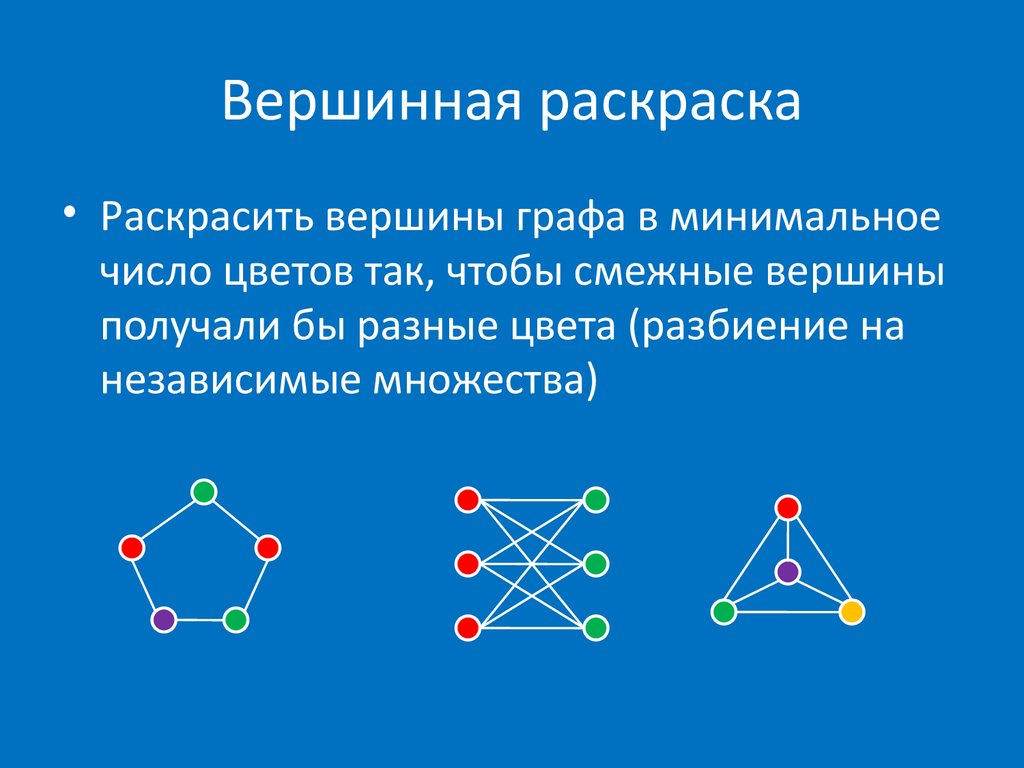
Раскраска графа — теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа , при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин.
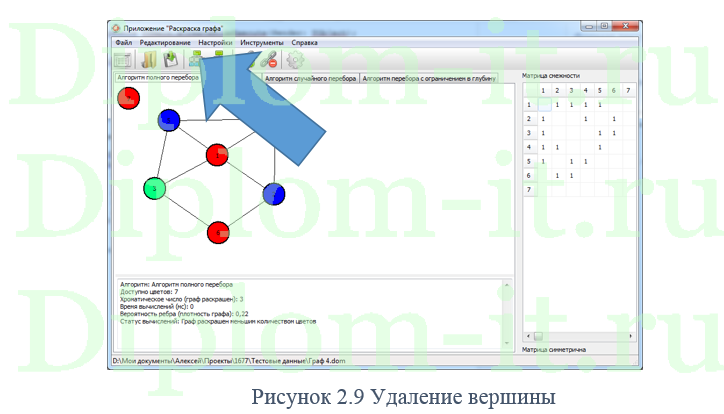
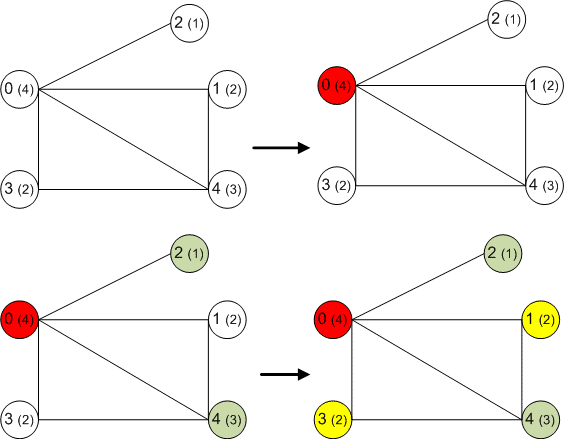
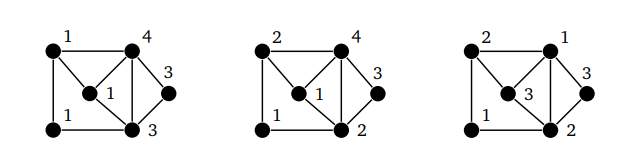
![Задачи сводимые к задачи раскраски [В работе] Конспект лекции по раскраскам](http://grafoanalizator.unick-soft.ru/help/html/helpgraf1.3_html_24ec2e8e.png)


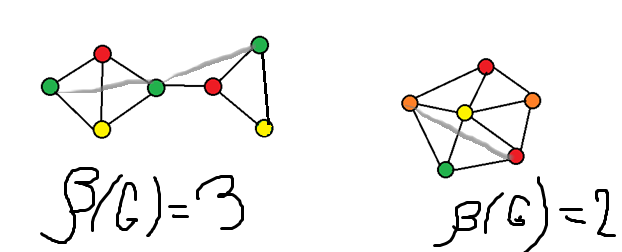

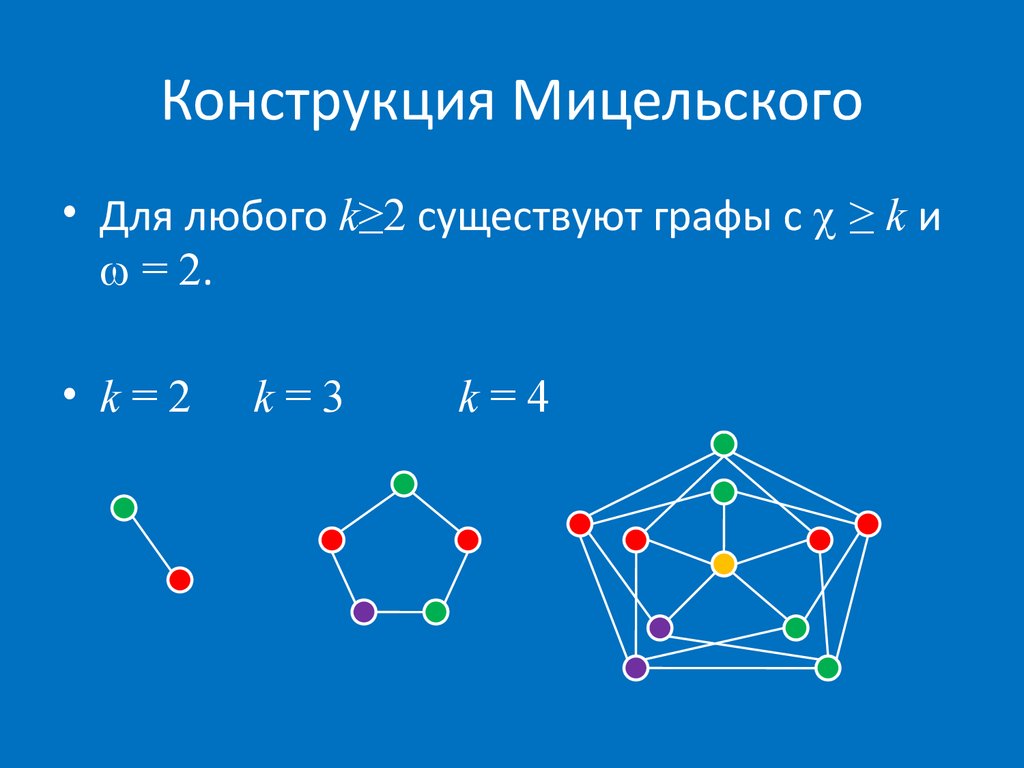
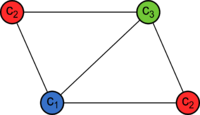
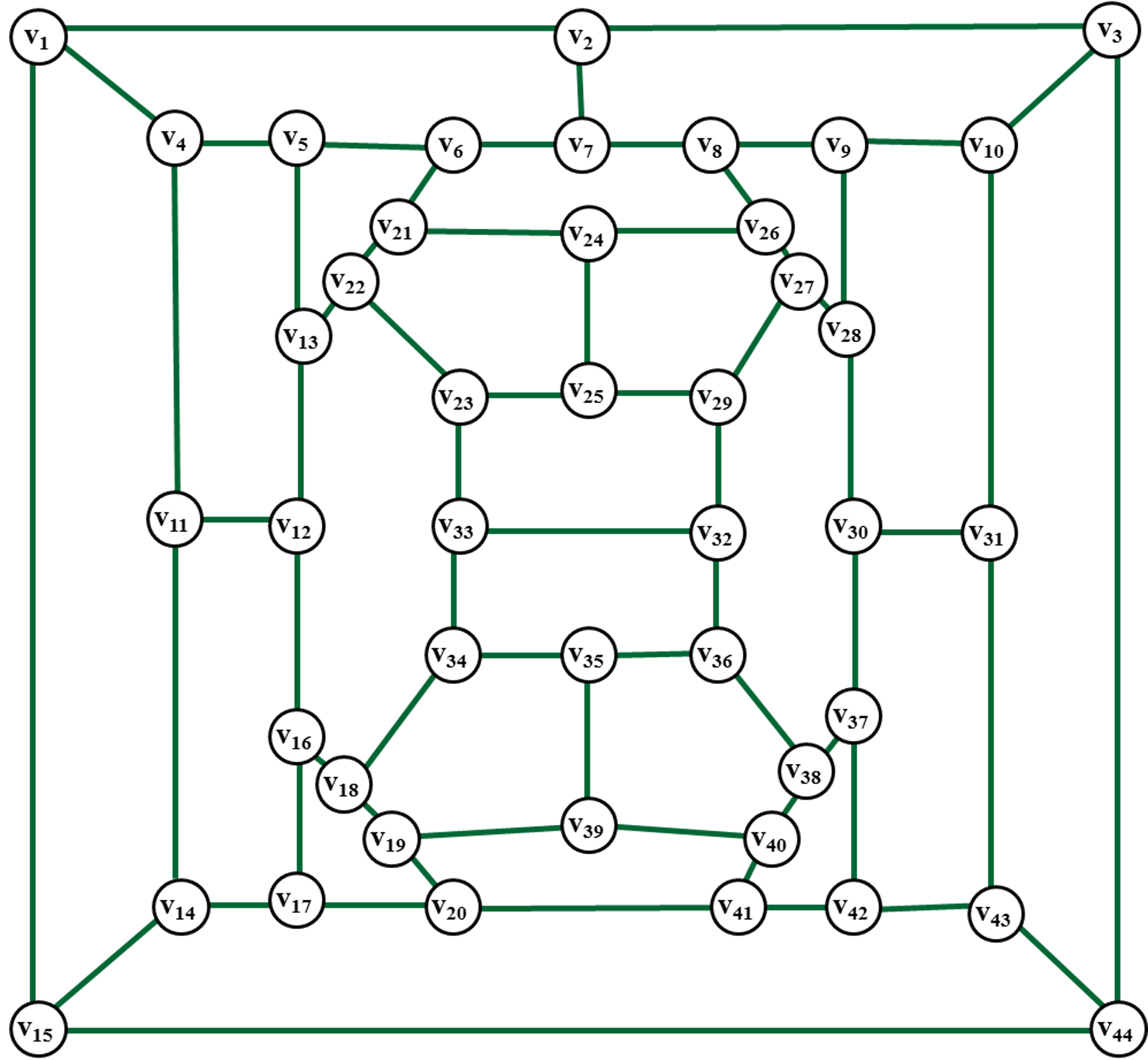


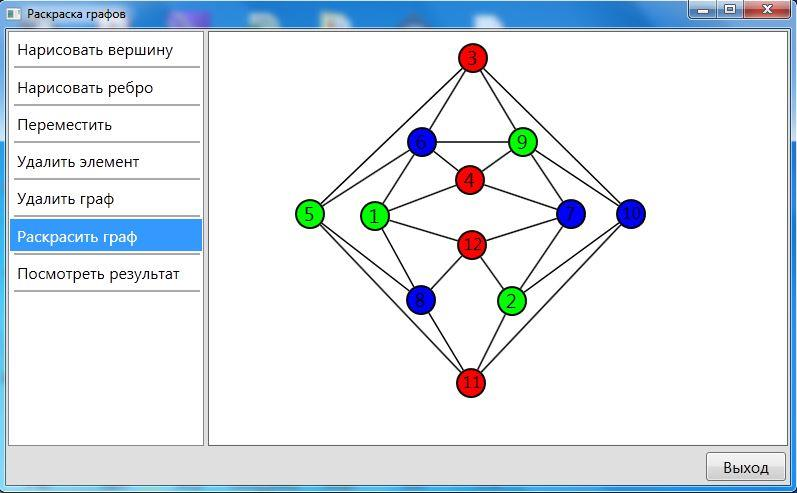
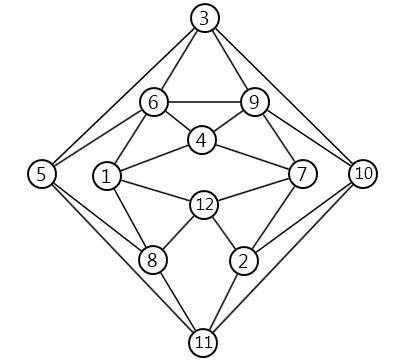
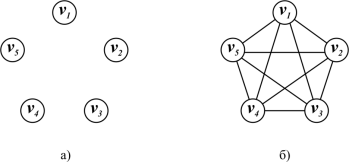
В этом уроке мы разберем, что такое раскраска графов и как это относится к цифрам на вершинах. Также покажем примеры раскраски графов разных типов, так как в каждом случае этот процесс немного отличается. Цвета — это целые положительные цифры.


![[В работе] Конспект лекции по раскраскам [МОЭВМ Вики [skproff-remont.ru]]](https://habrastorage.org/files/cec/055/bf4/cec055bf4010476b86a53a780e695076.png)



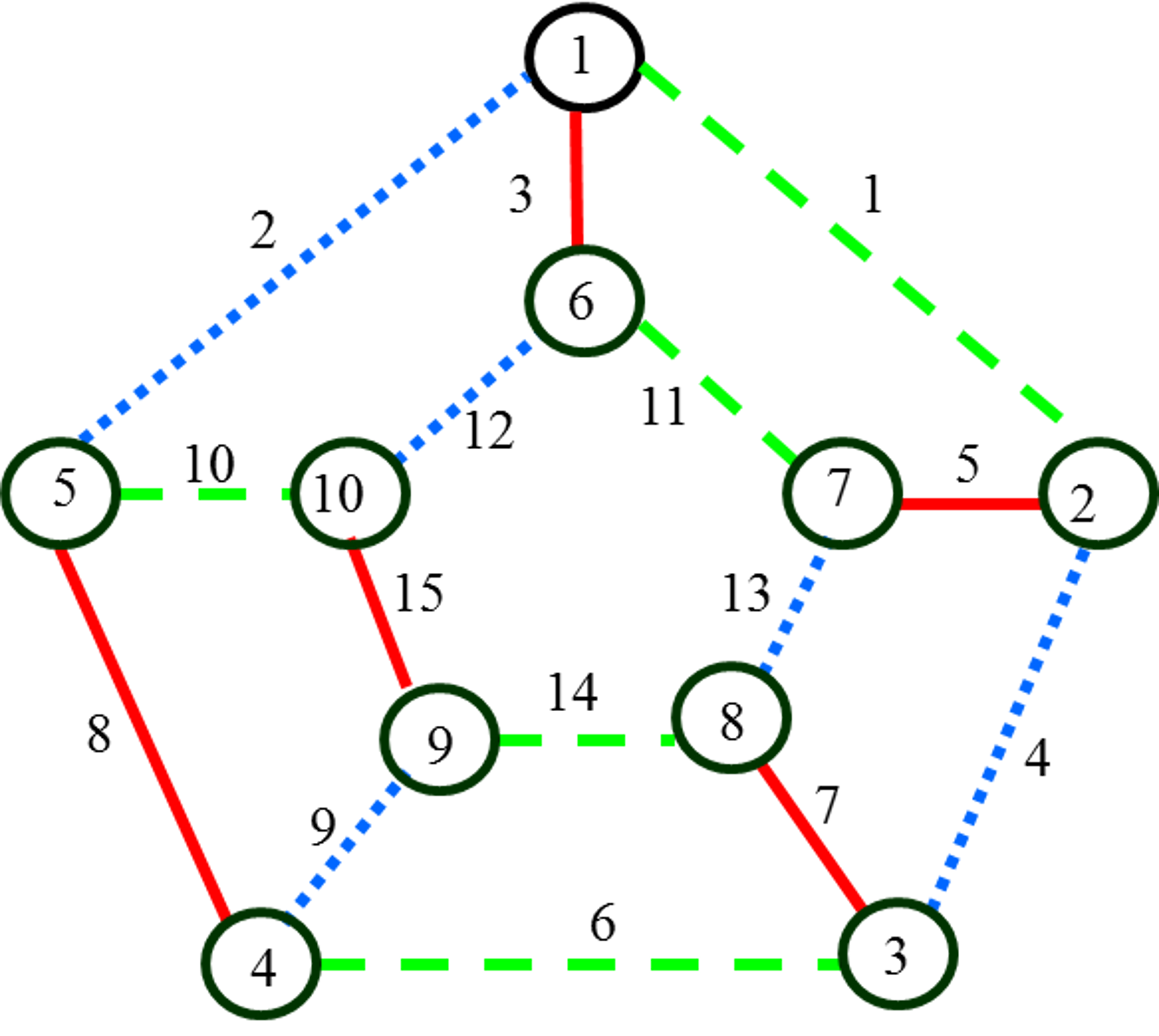
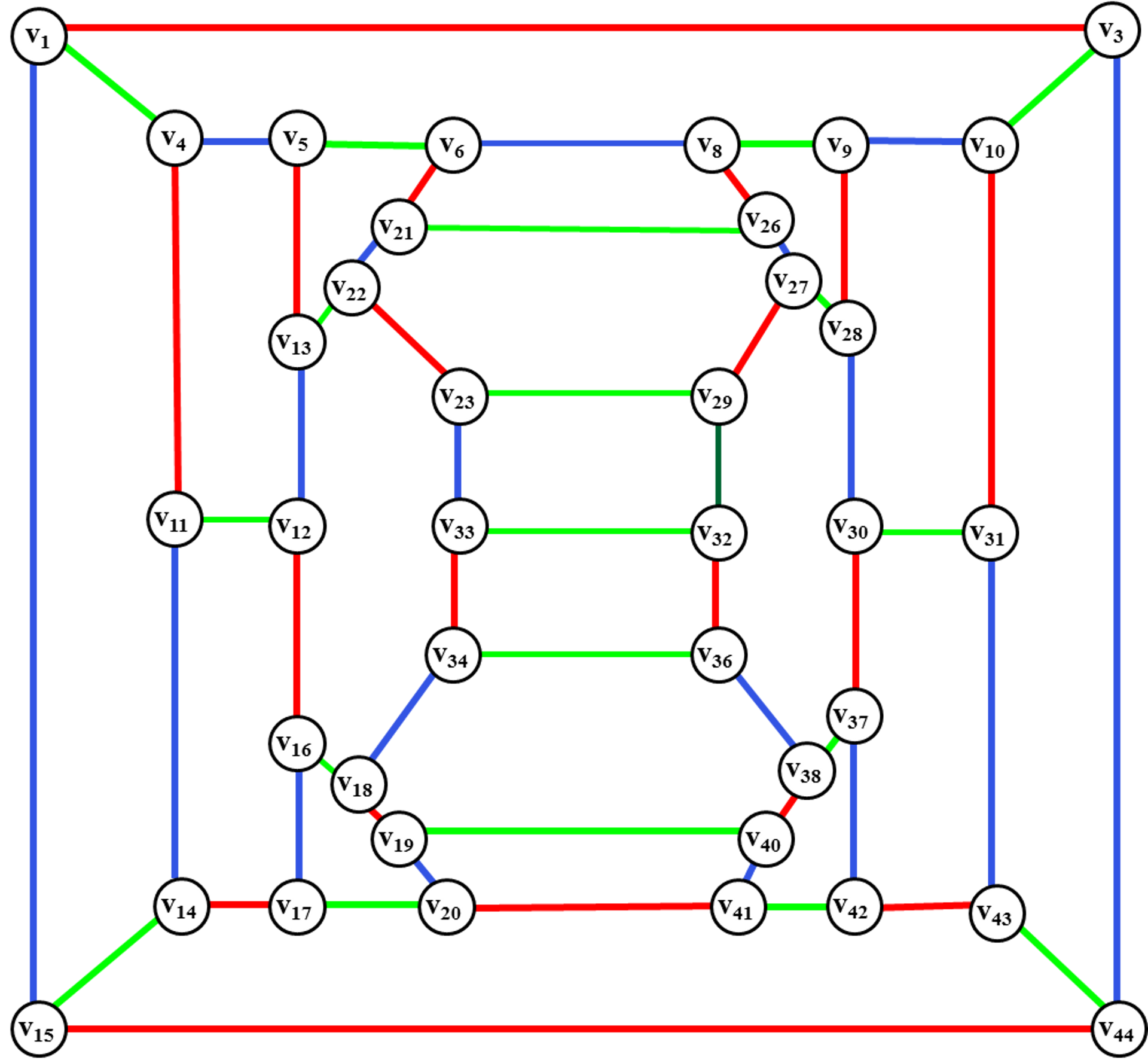
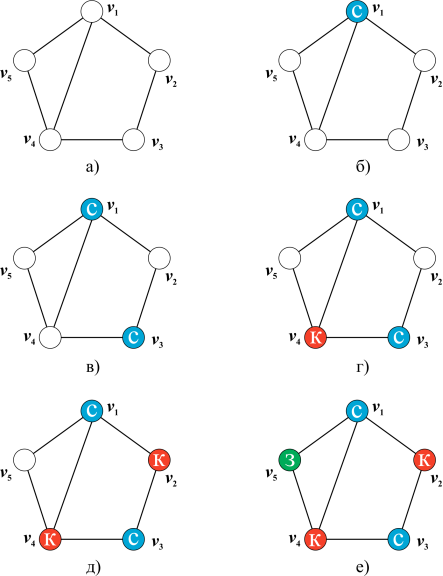
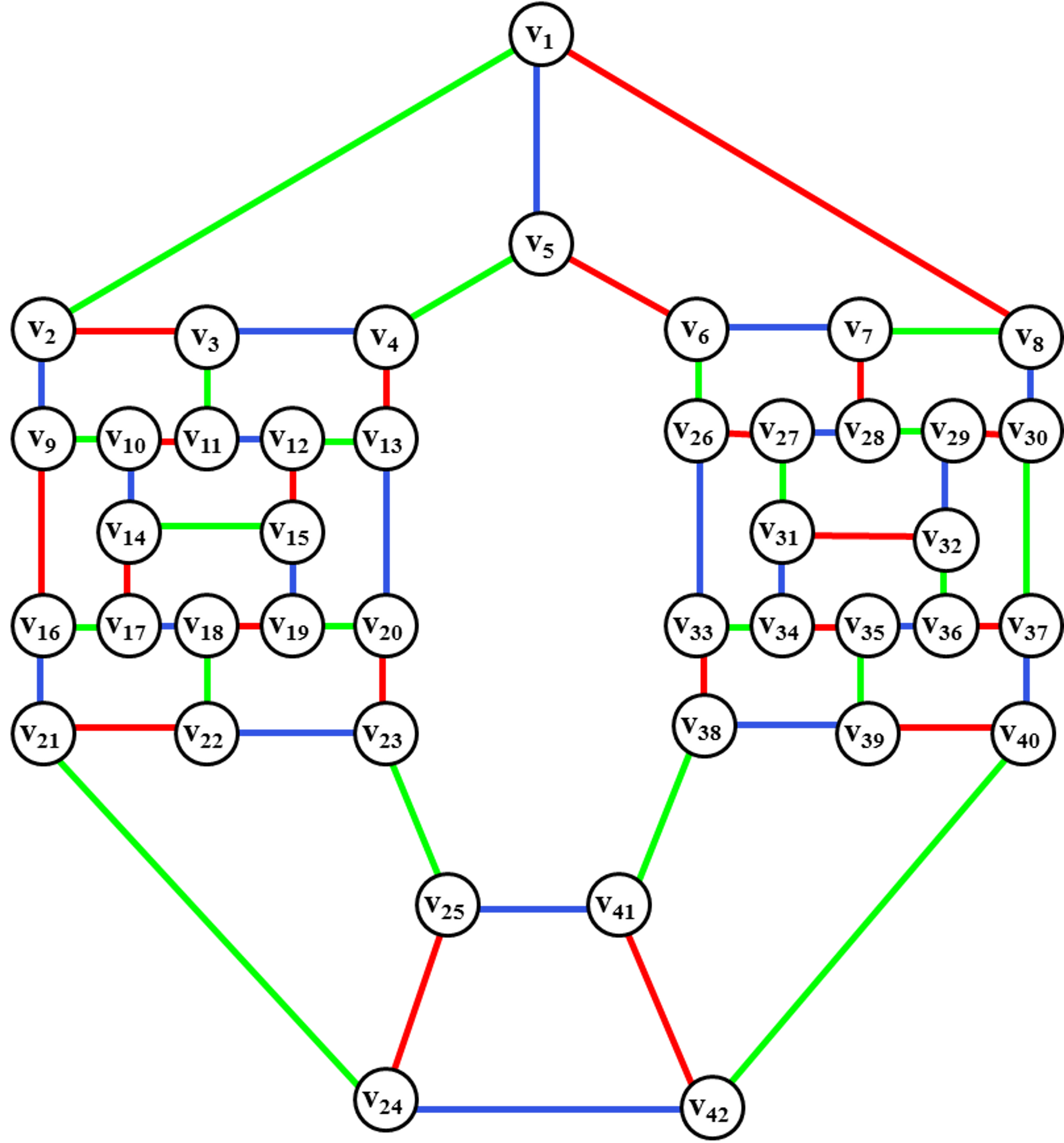
Жадная раскраска в теории графов — раскраска вершин неориентированного графа , созданная жадным алгоритмом , который проходит вершины графа в некоторой предопределённой последовательности и назначает каждой вершине первый доступный цвет. Жадные алгоритмы, в общем случае, не дают минимально возможное число цветов, однако они используются в математике в качестве техники доказательств других результатов, относящихся к раскраске, а также в компьютерных программах для получения раскраски с небольшим числом цветов. Корона полный двудольный граф K n , n с удалёнными рёбрами совершенного паросочетания является особенно плохим случаем для жадного алгоритма — если в последовательности вершин поместить подряд две вершины, принадлежащие удалённому ребру из паросочетания, жадный алгоритм использует n цветов, в то время, как оптимальным числом для такого графа является два цвета.